In this short book we, Open Privacy, will document our investigations into Fuzzy Message Detection, including extensions to the proposed scheme and simulation results when modelling realistic deployments.

Introduction to Fuzzytags

Anonymous messaging systems (and other privacy-preserving applications) often require a mechanism for one party to learn that another party has messaged them.

Many schemes rely on a bandwidth-intensive "download everything and attempt-decryption" approach. Others rely on a trusted 3rd party, or non-collusion assumptions, to provide a "private" service.

It would be awesome if we could get an untrusted, adversarial server to do the work for us without compromising metadata-resistance!

fuzzytags is an experimental probabilistic cryptographic tagging structure to do just that!

Specifically fuzzytags provides the following properties:

Correctness: Valid tags constructed for a specific public key will always validate when tested using a derived detection key.
Fuzziness: Tags will produce false positives with probability p related to the security property (γ) when tested against detection keys they were not intended for.
Security: An adversarial server with access to the detection key is unable to distinguish false positives from true positives. (Detection Ambiguity)

Formally

For an in depth analysis see the origin paper Fuzzy Message Detection by Gabrielle Beck and Julia Len and Ian Miers and Matthew Green.

Note, that paper uses multiplicative notation, throughout this book we will use additive notation.

All parties in the fuzzy tag system derive an ordered set of $γ$ secret keys $x$ and a public key $X = {x_{i} G : \forall x_{i} \in x}$

A fuzzytag consists of:

a ciphertext, $c$ , of length $γ$ ,
a group element: $U = r G$ , where $r$ is a random scalar.
and, a scalar: $y = r^{- 1} \times (z - m)$ where $z$ is another random scalar, and $m$ is a scalar derived from the output of a hash function over $u$ and the $c$ .

The ciphertext is obtained by constructing a key $k = {k_{i} = H (U ∣∣ r X_{i} ∣∣ w) \forall i \in X)}$ and calculating $c = k \oplus 1$

Checking a text is done over a detection key $d$ of length $n$ where $d = x_{0 \dots n}$ , this detection key can be given to an adversarial server to perform filtering.

$k$ is recalculated by first deriving $w$ using $u$ and $y$ and then calculating ${k_{i} = H (U ∣∣ x_{i} U ∣∣ w) \forall i \in x)}$ and the plaintext is recovered $p = k \oplus c$ and compared to $1$ .

Additional Checks

We perform the following additional checks when verifying a tag:

Discard tags that would validate for every single public key.
- We assert that $U$ is not the identity element.
- We assert that $y \neq = 0$
Reject tags intended for different setups:
- We include $γ$ in the input to both the $H$ and $G$ hash functions.

Terminology

Throughout this book, the fuzzytags API and documentation we use the following terms, some of which deviate and/or extend definitions from the original paper.

Tag

A probabilistic structure that can be attached to a message in order to identify the recipient. The focus of the fuzzytags system.

Root Secret

A privately generated set of secret scalars. Randomly generated.

Not to be confused with "secret/private key" in larger system integrations.

Tagging Key

A publicly distributed set of group elements used to construct a tag for a given party. Derived from the Root Secret.

Not to be confused with "public key" in larger system integrations.

Detection Key

A semi-public subvector of the Root Secret that is provided to an adversarial server in order to outsource identification of tags (with some pre-determined false positive rate).

Not to be confused with "verification" key in larger system integrations.

Risk Model

In this section we will document the risk model and attacks that will likely impact practical deployments of fuzzytags.

We assume a set of $n$ parties sending tags and messages through an untrusted server.

For some of the analysis in this notebook we will assume that the server has knowledge of the sender of each tag.

While this is not desirable in real-world deployments, being able to match tags to senders does allow us to derive bounds on worst case metadata leakage.

Intersection Attacks

One of the most basic attacks primitives for any kind of false positive based scheme is an intersection attack, where the set of peers that match one tag is intersected against another set of peets that matches a different tag.

Any kind of intersection attacks break this scheme, even for a small number of messages i.e. if you learn (through any means) that a specific set of messages are all likely for a single party, you can diff them against all other parties keys and very quickly isolate the intended recipient - in simulations of 100-1000 parties it can take as little as 3 messages - even with everyone selecting fairly high false positive rates.

The corollary of the above being that in intersection attacks your anonymity set is the number of users who download all messages. This has the interesting side effect: the more parties who download everything, the more the system can safely tolerate parties with small false-positive rates.

Statistical Attacks

Using some basic binomial probability we can use the false positive rate of reach receiver tag to calculate the probability of matching on at least X tags given the false positive rate. Using this we can find statistically unlikely matches e.g. a low-false positive key matching many tags in a given period.

This can be used to find receivers who likely received messages in a given period. This attack works regardless of how many parties are downloading everything, and is entirely dependent on the receiver choosing $p$ that is suboptimal for the number of messages they receive.

If it is possible to group tags by sender then we can perform a slightly better attack and ultimately learn the underlying social graph with fairly low false positive rates (in simulations we can learn 5-10% of the underlying connections with between 5-12% false positive rates.)

The method is the same as above, but look at the probability that a party would have matched at least X tags from a specific sender given their false positive rate.

Notably, this latter attack reveals something important about choosing parameters for fuzzytags - p must be chosen to take into account not just total number of messages, but total number of messages from a given source (or it must be assumed that the server will never be able to isolate tags from a given sender)

Deploying FuzzyTags Securely

The properties provided by this system are highly dependent on selecting a false positive rate p. In the following sections we will cover a number of considerations you should take into account when integrating fuzzytags into a larger privacy preserving application.

How bad is it to let people select their own false-positive rates?

The short answer is "it depends".

The longer answer:

When different parties have different false positive rates the server can calculate the skew between a party's ideal false positive rate and observed false positive rate.

That skew leaks information, especially given certain message distributions. Specifically it leaks parties who receive a larger proportion of system messages than their ideal false positive rate.

i.e. for low false positive rates and high message volume for a specific receiver, the adversarial server can calculate a skew that leaks the recipient of individual messages - breaking privacy for that receiver.

It also removes those messages from the pool of messages that an adversarial server needs to consider for other receivers. Effectively reducing the anonymity set for everyone else.

Should Senders use an anonymous communication network?

If statistical & differential attacks are likely e.g. few parties download everything and multiple messages are expected to originate from a sender to a receiver or there is other information that might otherwise link a set of messages to a sender or receiver then you may want to consider how to remove that context.

One potential way of removing context is by having senders send their message to the server through some kind of anonymous communication network e.g. a mixnet or tor.

Be warned: This may not eliminate all the context!

How bad is it to select a poor choice of p?

Consider a pareto distribution where most users only receive a few messages, and small subset of users receive a large number of messages it seems that increasing the number of parties is generally more important to overall anonymity of the system than any individual selection of p.

Under a certain threshold of parties, trivial breaks (i.e. tags that only match to a single party) are a bigger concern.

Assuming we have large number of parties (N), the following heuristic emerges:

Parties who only expect to receive a small number of messages can safely choose smaller false positive rates, up to a threshold θ, where θ > 2^-N. The lower the value of θ the greater the possibility of random trivial breaks for the party.
Parties who expect a large number of messages should choose to receive all messages for 2 reasons:
1. Even high false positive rates for power users result in information leaks to the server (due to the large skew) i.e. a server can trivially learn what users are power users.
2. By choosing to receive all messages, power users don't sacrifice much in terms of bandwidth, but will provide cover for parties who receive a small number of messages and who want a lower false-positive rate.

(We consider a pareto distribution here because we expect many applications to have parties that can be modelled as such - especially over short-time horizons)

Entangled Tags

It is possible to generate fuzzytags for a given $γ$ that are valid for 2 or more parties at the same time.

This is done through $FlagEntangled$ - a function that takes in a vector of tagging keys and runs the $Flag$ function, as documented in the original paper for each of them (with the same $r an d z$ ) until it finds a $z$ that will generate the same tag for every tagging key.

Here we briefly outline a number of properties of entangled tags. In the next section we will consider how to apply these strategies in real-world deployments.

Multiparty Broadcast

Alice wants to send a message to Bob and Carol. She constructs a single tag that will validate against detection keys generated by both of them.

When an adversarial server matches the tag against all the keys it knows about it will discover that the tag matches both Bob and Carol (in addition to some number of false positives depending on the false positive rates of all the other parties using the server).

To construct such a tag Alice runs $FlagEntangled({X_{bob}, X_{carol}})$ .

The adversarial server will match the tag to the detection keys of both Bob and Carol. The server has no way of determining if the match is a broadcast to both parties, a unique message to one of Bob or Carol or a false positive for both.

Deniable Sending

Alice wants to send a message to Carol, but is concerned that Carol may have a detection key with too low false positive rate. Alice knows of a set of parties (and their public keys) who also use the adversarial server to send privacy messages. Alice searches for a tag that will validate against detection keys generated not only by Carol but a randomly selected party e.g. Eve.

When an adversarial server matches the tag against all the keys it knows about it will discover that the tag matches both Carol and Eve (in addition to some number of false positives depending on the false positive rates of all the other parties using the server).

Even if the server was to isolate this specific message as originating from Alice, they would not be able to derive the recipient through any kind of differential attack (as all attacks would also implicate Eve).

To construct such a tag Alice runs $FlagEntangled({X_{carol}, X_{eve}})$ .

Alice could choose to entangle all of her messages to Carol in this way, fully implicating Eve in her message sending regardless of Eve's false positive rate. If Eve attempted to decrypt the message she would not be able to and might assume that the tag was an unlikely false positive - as such too many of these messages might cause Eve to be suspicious. However, Eve might be a well known service or bot integrated with the privacy preserving application - allowing Alice cover without worrying about triggering suspicion.

Alice could also choose to entangle each message with a different random party.

While this strategy is, by itself, vulnerable to intersection attacks; it increases the number of potential relationships any adversary needs to rule out in order to derive the resulting metadata from the communication.

When combined with a large number of parties downloading all messages (or even downloading with high false positive rates) this strategy has the effect of increasing the anonymity set of the entire system.

It is worth nothing at this point that strategies can be combined, and their effects compound. When given a tag and a set of matches an adversarial server cannot distinguish between a true and false positive, an entangled deniable send or a group broadcast - or a combination!

Forging False Positives

Alice wants to send a message to Carol, but also wants to implicate Eve to the server. However Alice doesn't have enough time or computing power to generate a tag that will fully match against Eve's full $γ$ -length key.

Instead Alice forges an entangled tag by running $FlagEntangled({X_{carol}, X_{eve}})$ , however, instead of checking all parts of the key at line $11$ she instead only checks up to a value $l$ that she believes is greater than or equal to the false positive rate of Eves detection key.

To the server the tag would match both to the detection key of both Carol and Eve, but when fetched Eve would assume it was a false positive (a much more likely one than in our previous example).

Entangling Strategies

In this section we will document a number of different strategies that applications might consider when implementing an entangling scheme. Where possible we will provide analysis and simulations to assess privacy impact of each one.

No Entangling

For completeness, let's consider no entangling. In this case each tag has a single recipient. We have shown through simulations that fuzzytags, in aggregate, leak information to the server. Being able to attribute a fuzzytag to a receiver with confidence reduces the false positive rate on the derived graph.

On the other hand, all entangling strategies require access to a global database of tagging keys in order to be effective - this has concrete privacy and security concerns in-and-of itself.

Random Entangling

One of the simplest schemes involves every sender selecting a single random entangled recipient. We have simulated this strategy against real world datasets and found that it does little to prevent the server from deriving the underlying social graph - only marginally increasing the false positive rate of connections on the derived graph.

To understand why, consider that entangling tags in this way doesn't create a signal intended to corrupt the derived graph, but instead adds noise to the number of received tags for each detection key. As the number of legitimate tags received increases, they create a signal that stands above the noise floor of the generated tags.

Deniable Entangling

As outlined in the last section, one of the major properties of entangled tags is deniable sending i.e. they make it possible to legitimately send a message to multiple parties.

One possible deployment approach is to have a one or more known popular services using fuzzytags to receive messages, and for all parties to entangle their messages to both the intended recipient and a popular service.

This approach provides two distinct benefits:

Only the tagging keys of popular services need to be known - these can be public and heavily popularized, discounting most security and privacy concerns with maintaining a database of keys to entangle to.
Every tag in this scheme is individually deniability, increasing the anonymity set of all received tags.
Such services provide a bootstrapping mechanism for a network based on fuzzytags

The one major drawback of this approach centres around the addition of a number of select service providers into the anonymity model resulting in a psuedo-non-collusion assumption, in addition to raising the spectre of compulsion attacks.

Both of these drawbacks can be mitigated through diversification of the entanglement pool - at it must be pointed out that unlike many non-collusion assumptions there is no direct systemic relationships between the adversarial server providing fuzzytags and services built on top of such a service i.e. anyone can start providing a service and anyone can start entangling to a service without these being core features to the anonymity system.

It must be stated that such an entangling scheme does not remove the risk that aggregate tags will reveal the underlying social network (as the signal is still there), it simply invokes a deniability argument for the relationship. This may be sufficient, but is not always going to be so.

As such any simulation of this approach will likely be identical to one for not-entangling at all - with the false positive result replaced with a deniability disclaimer.

Simulating fuzzytags

We also provide simulation software to experiment with various deployment of fuzzytags given certain system parameters like the number of parties, a model of message sending, and the rate of entangled tags.

In this section we will document simulations performed on the Email EU Core dataset (details below). In particular, we assess the worst-case scenario of a server with access to a sender-oracle (i.e. able to attribute tags to a particular sender) to understand how much information is leaked by fuzzytags without appropriate deployment mitigations.

Email EU Core Dataset Simulations

Nodes:              1004
Temporal Edges: 	332334
Time span:          803 days

Citation: Ashwin Paranjape, Austin R. Benson, and Jure Leskovec. "Motifs in Temporal Networks." In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, 2017.

Scenario 1

Setup: 1 month of email events between 1004 nodes, 20k events (5148 links). False positive rates: [0.007812, 0.5]. No entangling.

Result: An adversarial server can identify ~7% of original graph (393 links) with a 6% false positive rate. Threshold: 0.0001

Scenario 2

Setup: The same month of emails, 20k events (5148 links) Same false positive rates. Every tag is entangled with 1 random node.

Result: Server can identify ~6.6% of original graph with a 6.8% false positive rate.

Discussion

Entanglement seems to have some impact on the servers ability to relearn the social graph, in particular it increases the false positive rate of the derived graph. However, this impact is not significant enough in the observed simulation.

In this section we will document simulations performed on the College Msg Core dataset (details below). In particular, we assess the worst-case scenario of a server with access to a sender-oracle (i.e. able to attribute tags to a particular sender) to understand how much information is leaked by fuzzytags without appropriate deployment mitigations.

College IM Dataset Simulations

Nodes 	1899
Temporal Edges 	59835
Time span 	193 days

Pietro Panzarasa, Tore Opsahl, and Kathleen M. Carley. "Patterns and dynamics of users' behavior and interaction: Network analysis of an online community." Journal of the American Society for Information Science and Technology 60.5 (2009): 911-932.

Scenario 1

Setup: 20k events (7330 links). False positive rates: [0.007812, 0.5]. No entangling.

Result: Server can identify ~4.3% of original graph (313 links) with a 12% false positive rate at threshold: 0.0001.

Scenario 2

Setup: 20k events (7330 links). False positive rates: [0.007812, 0.5]. Every tag entangled to one random node (as before).

Result: Server can identify ~3.95% of original graph (290 links) with a ~15% false positive rate.

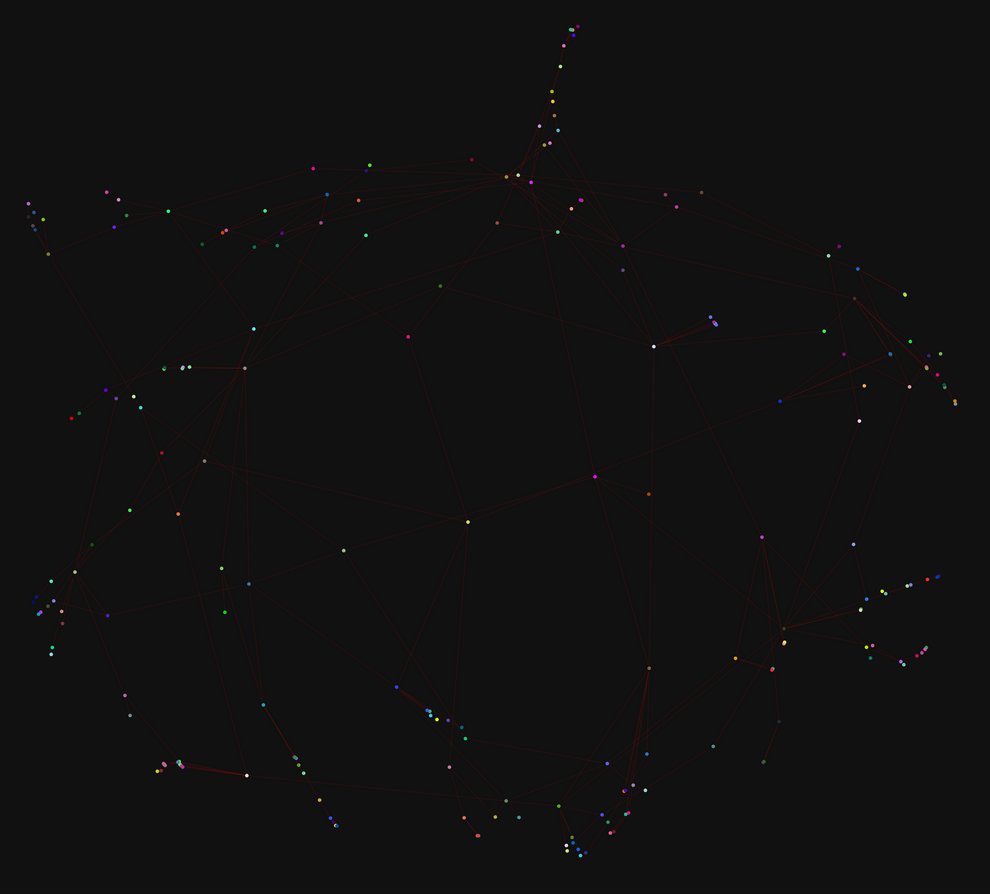
Discussion

A very similar result to our observations on the EU Core email dataset, entangled tags increase the false positive rate, although overall it requires non-naive entangling strategies to push the false positive rate of the derived graph to a place where it would not be useful for an adversary.

FuzzyTags: The Book